Das Acht-Damen-Problem

Ich bin über eine Programmierübung gestolpert, welche zu Beginn meines Studiums gestellt wurde. Bei dieser Aufgabe geht es darum, alle Möglichkeiten zu finden, bei denen acht Damen auf dem Schachbrett platziert werden, ohne dass sie sich gegenseitig schlagen.
Ich hab mir dafür das Schachbrett mit einer X- und Y-Achse vorgestellt und setze im Programm in der Reihe X0 nacheinander alle Damen.
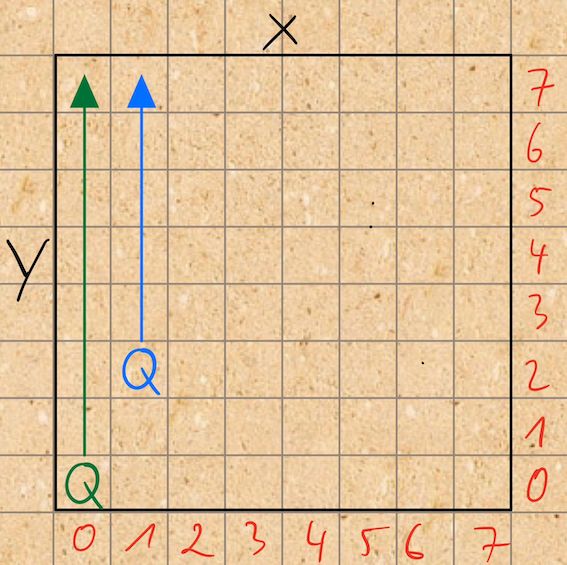
Wenn die erste Dame gesetzt wurde, werden anschließend von Reihe X1-X7 alle restlichen Damen rekursiv gesetzt. Falls in einer Reihe keine Dame mehr gesetzt werden kann, folgt kein rekursiver Aufruf mehr und es gibt keine Lösung mit den vorher gesetzten Damen. Anschließend wird versucht die zuletzt gesetzte Dame ein Feld weiter zu setzen.
#include <iostream>
#include <vector>
size_t count = 0;
void printField( std::vector<unsigned>& field ){
for ( size_t i = 0; i < field.size(); ++i ){
for ( size_t j = 0; j < field.size(); ++j ){
std::cout << ( field.at(j) == i ? "Q ": "- " );
}
std::cout << std::endl;
}
std::cout << std::endl;
}
bool testAll( std::vector<unsigned>& field, unsigned y,
unsigned queensSet ){
for( int x = 0; x < queensSet; ++x ){
if( field.at(x) == y //waagerechte Prüfung
||field.at(x) == y-( queensSet - x ) //diagonale Prüfung
|| field.at(x) == y+( queensSet - x ) ){ //diagonale Prüfung
return false;
}
}
return true;
}
//Rekursive Funktion
void setQueenRec( std::vector<unsigned>& field, unsigned queensSet ){
//wenn alle Damen gesetzt wurden
if( queensSet == field.size() ){
++::count;
printField(field);
return;
}
for( int y = 0; y < field.size(); ++y ){
//Test, ob die Dame in der nächsten Reihe gesetzt werden kann
if( testAll( field, y, queensSet ) ) {
field.at( queensSet ) = y;
setQueenRec( field, queensSet+1 );
}
}
}
void setQueen( std::vector<unsigned>& field ){
for( int y = 0; y < field.size(); ++y ){
field.at(0) = y;
//in der erste Reihe werden nacheinander die Damen gesetzt
setQueenRec( field, 1 );
}
}
int main() {
//speichert die Positionen der Damen
std::vector<unsigned> field( 8, 0 );
setQueen( field );
std::cout << "Lösungen insgesamt: " << ::count<< std::endl;
return 0;
}Bei dieser Lösung werden auch gespiegelte und 90° gedrehte Felder mitgezählt. Daher beträgt bei mir die Anzahl der Möglichkeiten 92 und die Anzahl der eindeutigen Lösung beträgt 12.
